What is NumPy?
- The core library for scientific computing
- Provides a new data structure called an “array”
- It is like a list, but more efficient
- Provides many functions that work with NumPy arrays
- https://numpy.org
Installing NumPy
- If you use Thonny, go to Tools -> Manage packages. Type numpy in the search bar and click “Search on PyPI”. Then click Install.
- If you do not have Thonny, you can do so by typing the following commands in the terminal:
python -m pip install -U pip python -m pip install -U numpy
What is a NumPy array?
- A NumPy array is a multidimensional collection/grid of items of same type .
- Multidimensional: it could be a linear array (like a list e.g. vector) or a 2D array (like a list of lists e.g. matrix), 3D array etc.
- Unlike a regular Python list,
- All the values in a NumPy array must have the same type.
- A NumPy array’s size cannot be changed after creation.
- All such operations that change the size (e.g. adding/removing items) result in a copy of the array.
Creating an array
1import numpy as np23# Create a NumPy array from a Python list4arr = np.array([1, 2, 3])5print(arr)6# [1 2 3]7# note the lack of commas in the output89print(type(arr)) # <class 'numpy.ndarray'>1011# convert a tuple object to numpy array12x = np.array((1, 10, 100))13print(x) # [ 1 10 100]
We can specify the data type of elements when creating an array.
1import numpy as np23# these floats will be converted to ints (by truncation)4x = np.array([1.2, 3.14, 10.65], dtype=int)5print(x) # [ 1 3 10]6print(x.dtype) # int6478# We can also specify a NumPy-defined data type9x = np.array([10, 20, 30], dtype=np.float64)10print(x) # [10. 20. 30.]11print(x.dtype) # float64
Shape and dimensions of a NumPy array
- The number of dimensions is how many levels of nested arrays there are. e.g. 1D array, 2D array, etc. It can be obtained by accessing the ndim attribute.
- shape attribute of a NumPy array is a tuple containing size/length in each dimension.
1import numpy as np23x = np.array([10, 20, 30])45print(x.ndim) # 16print(x.shape) # (3,)
1import numpy as np23x = np.array([[10, 20, 30], [40, 50, 60]])4print(x)5# [[10 20 30]6# [40 50 60]]78print(x.ndim) # 29print(x.shape) # (2, 3) <-- row, col
Indexing a NumPy array
1import numpy as np23arr = np.array([2, 4, 8])4print(arr[0], arr[1], arr[2]) # 2 4 856# we can modify existing elements.7arr[0] = 18print(arr) # [1 4 8]
Other ways to create arrays
1import numpy as np23# create an array of 0's, with shape (2,).4x = np.zeros(2)5print(x)6# [0. 0.]7# dots above mean float values89# create an array of all 1's, with shape (3,),10# of integer type.11y = np.ones(3, dtype=int)12print(y) # [1 1 1]
1# create an array of shape (5,) filled with one value2x = np.full(5, 7)3print(x)4# [7 7 7 7 7]56# create an array of 4 random values in the interval [0.0, 1.0).7y = np.random.random(4)8print(y)9[0.70260439 0.68529032 0.59847495 0.88655089]
Some useful numpy functions
1import numpy as np23# Similar to the built-in range() function,4# we can use arguments start, stop and step.5x = np.arange(10)6print(x)7# [0 1 2 3 4 5 6 7 8 9]89# Unlike range(), float numbers are allowed.10x = np.arange(10.0, 20.0, 2.5)11print(x)12# [10. 12.5 15. 17.5]
When we want to create a list of evenly-spaced numbers, it is better to use np.linspace() than np.arange().
1import numpy as np23# Create an array of 5 evenly spaced numbers in interval [0, 1]4x = np.linspace(0, 1, 5)5print(x)6# [0. 0.25 0.5 0.75 1. ]78# 7 evenly spaced numbers in interval [10, 100]9x = np.linspace(10, 100, 7)10print(x)11# [ 10. 25. 40. 55. 70. 85. 100.]
Broadcasting operations
- An arithmetic operation between an array and a scalar (number) is applied to all elements of the array. It is known as broadcasting.
- It does not modify the given array; instead a new copy is created.
1import numpy as np2arr = np.linspace(-1.0, 5.0, 7)3print(arr) # [-1. 0. 1. 2. 3. 4. 5.]45# Multiplication is broadcasted to each element.6print(arr * 6) # [-6. 0. 6. 12. 18. 24. 30.]
1# Unary minus2print(-arr)3# [ 1. -0. -1. -2. -3. -4. -5.]45# Other operators work in same way6print(arr / 5)7# [-0.2 0. 0.2 0.4 0.6 0.8 1. ]89print(arr + 4)10# [3. 4. 5. 6. 7. 8. 9.]1112print((arr + 3) * 2)13# [ 4. 6. 8. 10. 12. 14. 16.]
Unlike Python lists, NumPy arrays implement operators such as * to perform arithmetic operations.
1import numpy as np23x = [1, 2, 3] # Python list4y = x * 55print(y)6# [1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3]78x = np.array([1, 2, 3])9y = x * 510print(y)11# [ 5 10 15]
NumPy also defines math functions that broadcast to all elements in the array.
1import numpy as np23arr = np.linspace(-1.0, 5.0, 7)45print(np.sin(arr))6# [-0.841 0. 0.841 0.909 0.141 -0.757 -0.959]78print(np.exp(arr)) # e^x function9# [ 0.368 1. 2.718 7.389 20.086 54.598 148.413]
Vector operations
An arithmetic operation between arrays is done element-wise. It is also called a vectorized operation.
1import numpy as np23a = np.array([34.0, -12.0, 5.0])4b = np.array([68.0, 5.0, 20.0])5print(a + b) # [102. -7. 25.]6print(a / b) # [ 0.5 -2.4 0.25]
Example
Write code to evaluate the expression below using NumPy:
s=k=0∑100100kπsin100kπ
1import numpy as np23k = np.arange(0, 101)4x = k * (np.pi / 100)5s = np.sum(np.sqrt(x) * np.sin(x))6print(s) # 77.51389798916512
Comparing the performance of numpy vs pure python solution
1import numpy as np2import time34start = time.time()56N = 100000007k = np.arange(0, N+1)8x = k * (np.pi / N)9s = np.sum(np.sqrt(x) * np.sin(x))10print(s)1112print("Time:", time.time() - start)
1import math2import time34start = time.time()56N = 100000007s = 08for k in range(0, N+1):9 x = k * (math.pi / N)10 s += math.sqrt(x) * math.sin(x)11print(s)1213print("Time:", time.time() - start)
Slicing NumPy arrays
Similar to lists, we can slice a 1D NumPy array.
1import numpy as np23y = np.array([0.0, 1.3, 5.0 , 10.9, 18.9, 28.7, 40.0])4print(y[1:4]) # print from index 1 until but not including index 45# [ 1.3 5. 10.9]67print(y[::-1]) # reversed copy8# [40. 28.7 18.9 10.9 5. 1.3 0. ]
Copying NumPy arrays
- We can use the array.copy() method to get a copy of an array.
- Changes to the copy will not affect the original array.
1import numpy as np23a = np.array([[1, 2, 3], [4, 5, 6]])45b = a.copy()6b[1][2] = 10078print(a)9print(b)
Output
[[1 2 3] [4 5 6]] [[ 1 2 3] [ 4 5 100]]
Matrix in form of a 2D NumPy array
1import numpy as np23# convert a list of lists into 2D NumPy array4m = np.array([[1, 2, 3], [4, 5, 6]])5print(m)6# [[1 2 3]7# [4 5 6]]89# create an array of all 0's of shape (2, 2).10# By default, dtype is float64.11print(np.zeros((2, 2))) # (2, 2) is a tuple.12# [[0. 0.]13# [0. 0.]]
1import numpy as np2# create an array full of 7's, of shape (2, 3).3print(np.full((2, 3), 7))4# [[7 7 7]5# [7 7 7]]67# create an array of random values in interval [0, 1).8print(np.random.random((2, 2)))9# [[0.1782372 0.35920979]10# [0.9368368 0.9005017 ]]1112# create an identity matrix of shape (3, 3).13print(np.eye(3))14# [[1. 0. 0.]15# [0. 1. 0.]16# [0. 0. 1.]]
Reshaping arrays
1import numpy as np23# We can also create a matrix from a 1D array, using np.reshape()4c = np.arange(6)5print(c) # [0 1 2 3 4 5]67# change the shape to (2, 3).8d = np.reshape(c, (2, 3))9print(d)10# [[0 1 2]11# [3 4 5]]
Indexing a 2D array
We can index into a multi-dimensional NumPy array by providing a comma-separated list of the indices.
1import numpy as np23m = np.array([[1, 2, 3], [4, 5, 6]])4print(m.shape) # (2, 3)56print(m[0, 0]) # 17print(m[0, 1]) # 28print(m[1, 0]) # 49print(m[1, 2]) # 6
Matrix (2D array) operations
1import numpy as np23# Broadcasting4b = np.array([[1, 4, 5], [9, 7, 4]])5print(2 + b)6# [[ 3 6 7]7# [11 9 6]]89print(np.sin(b))10# [[ 0.841 -0.757 -0.959]11# [ 0.412 0.657 -0.757]]
1import numpy as np23# Element-wise product of matrices4b = np.array([[1, 4, 5], [9, 7, 4]])5c = np.array([[0, 1, 2], [3, 4, 5]])67# Note: both matrices must have the same shape8print(b * c)9# [[ 0 4 10]10# [27 28 20]]
To perform matrix multiplication, we use the dot() function.
1import numpy as np23b = np.array([[1, 4, 5], [9, 7, 4]])4d = np.array([[ 4, 2], [ 9, 8], [-3, 6]])56# shapes must be (M, N) dot (N, P) --> (M, P)7print(np.dot(b, d))8# [[25 64]9# [87 98]]
Slicing a 2D array
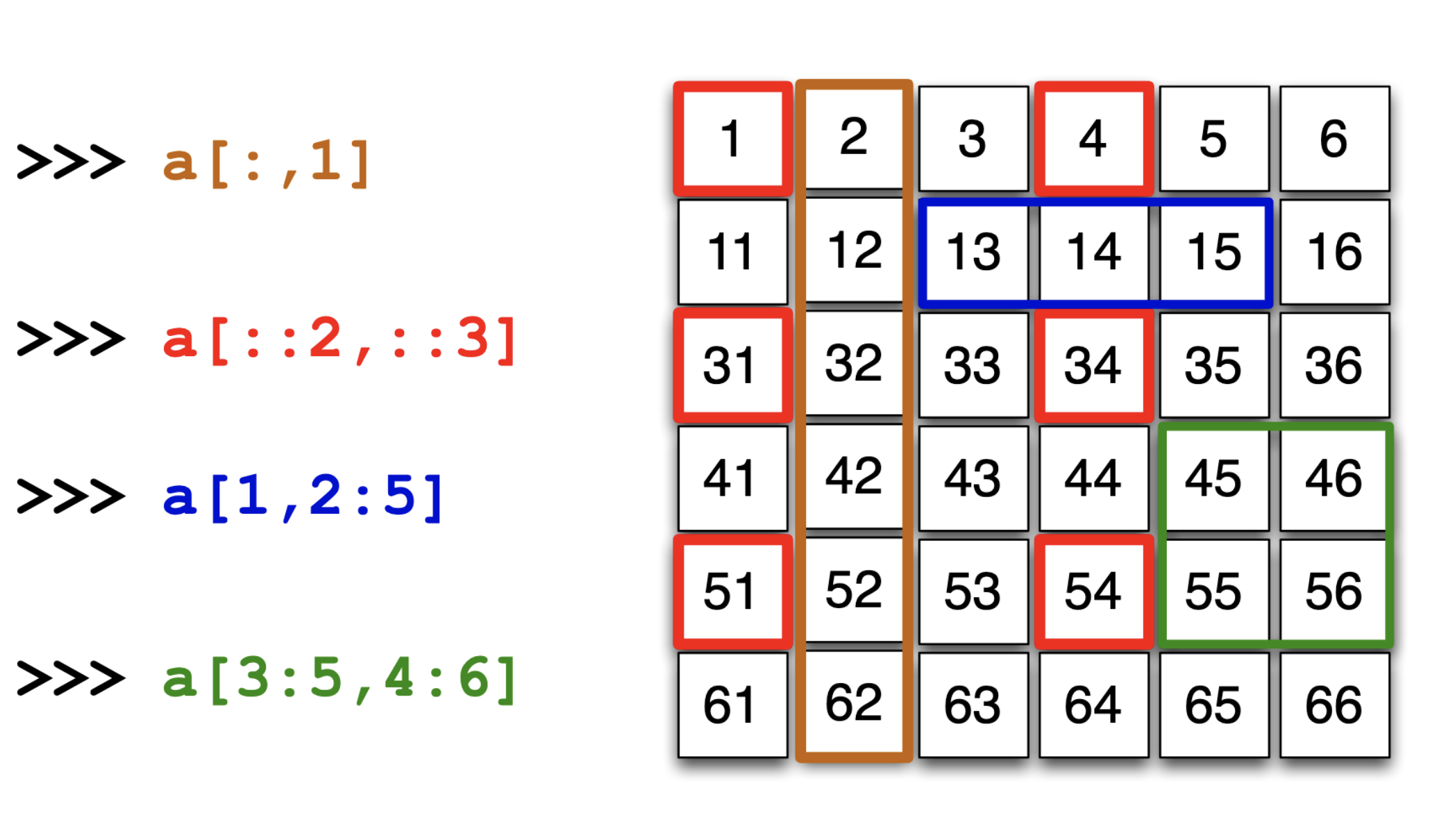
1import numpy as np23a = np.array([[ 1, 2, 3, 4, 5, 6],4 [11, 12, 13, 14, 15, 16],5 [31, 32, 33, 34, 35, 36],6 [41, 42, 43, 44, 45, 46],7 [51, 52, 53, 54, 55, 56],8 [61, 62, 63, 64, 65, 66]])910print(a[:, 1])11# [ 2 12 32 42 52 62]1213print(a[::2, ::3])14# [[ 1 4]15# [31 34]16# [51 54]]
1import numpy as np23a = np.array([[ 1, 2, 3, 4, 5, 6],4 [11, 12, 13, 14, 15, 16],5 [31, 32, 33, 34, 35, 36],6 [41, 42, 43, 44, 45, 46],7 [51, 52, 53, 54, 55, 56],8 [61, 62, 63, 64, 65, 66]])910print(a[1, 2:5])11# [13 14 15]1213print(a[3:5, 4:6])14# [[45 46]15# [55 56]]